第五十二卷

欽定古今圖書集成曆象彙編曆法典

　第五十二卷目錄

　曆法總部彙考五十二

　　新法曆書二〈恆星曆指一〉

曆法典第五十二卷

曆法總部彙考五十二

新法曆書二

恆星曆指一

「曆，以齊七政，乃自《日躔》而後，首論恆星者，何也？」曰：「日 躔終古行黃道，其經其緯易定耳。若月五星，各有道， 各有極，各有交，各有轉，粉糅不齊，非先定恆星之經 緯，即六曜之經緯，無從可論。故六曜如乘傳，恆星其 地誌也；六曜如行棋，恆星其楸局也。以是先恆星也。 恆星之黃道赤道須並論者，何也？」曰：「赤道在天中，終」 古不變，推步者賴為準則焉。乃諸曜皆循黃道行，一 切躔度因之布算。故用赤道經緯以求合於天元，用 黃道經緯以求合於本行，則七政如海舟。黃道其行 程，赤道其望山也，故黃赤二道須並論也。二道之兼 求經緯何也？曰：「凡測量躔度及交食會合，必將定其 所至之處，左右前後，纖微乖舛，非定處矣。故二道之 各經各緯，如棋局之有縱有橫，地圖之有袤有廣，闕 其一固不可也。」然則自古曆家何以皆有經度無緯 度乎？曰：「創始難工，增修易善。前人所作，為後人之師， 前人所缺，待後人而補。凡事盡然，曆為尤甚者，天事 難明故也。有經無緯，正前人所未及。《回回曆》有經有 緯，而成法為千年前所立，至今無測候改定者，亦彼 法所未及也。」曰：「繇前取喻，既以為郵之誌，棋之局，宜 恆定不易矣。今又須測候改定，則是恆星之經緯，亦 非恆定也。已自不定，曷為他行，待彼而定。」曰：「天載無 窮，天能無盡，大圜在上，既為動體，凡在體中，無有不 動。若云不動，則有窮之屬也。顧其為動，動必有法，若 云無法，又無能之屬也。天豈然哉？非止動而已也。」凡 能動者，皆有四端：一曰隨動，一曰自動，一曰疾動，一 曰遲動。宗動西行，諸曜從之，此隨動也。七曜恆星，各 自東行而各有法，此自動也。西行一日一周，其為亟 速，非思議所及，此疾動也。諸曜東行，經時不等，比於 宗動，皆可名遲。最遲者二萬五千餘年，而東行一周， 此遲動也。今論恆星，則屬自動，又屬遲動。自動既有 法，即依法推步，可為他行之法。遲動即數十年而微 露端倪，數百年而灼見違離。違離之後，因可隨時革 正。端倪初見，不妨豫為更易。其或甄明此學，人不絕 世，即數年之間，一為推變，有何不可？向所云測候改 定，職此之繇。《易》稱「治曆明時，取象於《革》。」至哉乎！一言 蔽之矣。曰：「向言每一動者，各有四動，今恆星之黃赤 經緯又屬四種。此四動者，異乎同乎？」曰：「安得同乎？黃 赤二道，位置不等，其各兩極不等，二經二緯，縱橫不 等，交互不等，故令星行不等，其差亦不等。有名為有 差，而絕不可謂差者，黃道之經度是也。恆星依黃道 東行，如載」籍相傳堯時冬至，日躔約在虛七度，今躔 箕四度，四千年間而日退行若干度者，即星之進行 若干度也。古曆謂之歲差，各立年率，郭守敬以為六 十六年有奇而差一度，今者斟酌異同，辨析微眇，定 為每歲東行一分四十三秒七十三微二十六纖。六 十九年一百九十一日七十三刻而行一度，凡「二萬 五千二百○二年九十一日二十五刻而行天一周， 終古恆然也。」此立名為差，而實有定法，不可謂差者 也。有行度不爽，而兩道參差，致生違異者，赤道之經 度是也。星依黃道行，與赤道諸緯皆以斜角相遇，兩 經相較，是生廣狹。因其廣狹，是生疾遲。又因其斜迤， 而從赤極分經，古今各測，復生參「錯，其南北東西，亟 舒寬迮，互有乘除，一再迴易，即還故處。」此則星經不 異，而以交道為異者也。有星本平行，而兩距變易，致 成升降者，赤道之緯度是也。黃赤兩至之距，為二十 三度八十六分有奇。星從南至，行北距如是，既迄象 限，與赤同行，迨於半周，則其距南亦復乃爾。計行半 周，而南北距差四「十七度七十二分有奇，盡一周而 復。」是其星行不異，而以距度為異者也。至若黃赤二 道兩至之距，古來皆稱二十四度，今測定為二十三 度八十六分七十六秒。考之《西史》所載，周顯王時一 測，西漢景帝時一測，東漢順帝時一測，三史折衷為 二十四度一十八分三十秒，以較今測差三十一分 五十四秒，此為二道之兩至距度，二千年間昔遠今 近，漸次移易之數也。故有不係星行，不關經度，而躔 道自為近就者，黃道之緯度是也。合四者論之，有易 見易知者一，有難見而可知者二，有易見而不可知 者一，黃道經行與日躔同類，理明數順，易見易知矣赤經、赤緯，糾紛轉易，致為繁曲；然其理可推，其數可 循，總皆二萬五千二百○二年有奇，而一周則難見 而可知也。惟是黃緯一差，分數曉然。然古時既遠，上 古時當更遠，不知遠於何始？今時既近，後來者當更 近，不知近於何終？遠極或當先近，不知改於何年；近 極或當返遠，不知轉於何日。此則非理數所能窮，非 思路所能及，故曰「『《易》見也，不可知也』。而近世曆家以 支離之詞，文鹵莽之術，揣摩者尚云微有移動，誕妄 者直曰天度失行。自非博稽遠覽，探賾索隱，何繇知 天運之必無僭差，天事之終難究竟耶？然則法當何 如？」曰：「無他道焉。深論理明，著數精，擇人審，造器隨時， 測驗追合於天而已。《西曆》所載恆星經緯，定自萬曆 年間，迄今已三十餘載，不敢因仍妄用。今擬新曆，以 崇禎元年戊辰歲為曆元，一切撰造，斷以是年為始。 故恆星黃赤道經緯，皆用是年實躔度分。展轉推算， 三四較勘，無有差忒，然後繪圖立表，以待施用。」別為 《恆星曆指》三卷。首言測驗諸法，次言本行及經緯度 變易，又次言經緯相求繪圖法義，於所謂深論理，明 著數者，未及詳備，已得其十二三矣。用之百年，當無 舛戾。後此依法推變，略如前說，凡為圖二十有五，立 成表四卷。其與舊傳天文圖稍異者，舊圖無緯度并 分宮分宿，一千二百年前所定，今則皆係見測。又圖 中止有形象而無本星躔度，《回回曆立成》所載有黃 道經緯度者止二百七十八星，「其繪圖者止十七座， 九十四星，亦無赤道經緯。今皆崇禎元年所測黃、赤 二道經緯度分，各各備具，各各正對。一加量度」，即圖 中各星所在度分，與《立成表》所載本星度分各各符 同，並無差失。凡有測而入表者一千三百五十六星， 所分大小等次，遠近位置，紆直形模，悉與天象相合。 其所繇符合者，非從舊圖改易，非從懸象倣摹。若改 易倣摹，不惟不合，且去之彌遠。今此諸圖黃赤經緯， 每座每星測算既確，次於圖中，依表點定，乃加印記， 後方聯綴，所謂「閉門造車，出而合轍。」因此知前之測 候，曾無乖爽，後來致用，可無謬誤也。其舊圖未載，而 體勢明晳、測量已定、經緯悉具者，一一增入舊圖所 有而微細隱約者，雖仍其位座，目所未見，星猶闕焉。 此外微星雖分明可見，而不在測數者，悉無增加，免 致煩亂。至若舊圖中南天田、六甲、天柱、天床等星，皆 茫昧依希，不成位座。又如器府、天理、八魁、天廟等星， 按圖索之，了不可得，其近處多有微星。或云「昔之作 者，牽合此星，綴緝成形，以補苴空缺。」今欲依經緯度 分聯之，即非本像，因仍舊貫，則飾無為有，跡涉矯誣。 儻令依圖指陳，依法測驗，將無辭以對，不得不并廢 其名也。

《測恆星法》第一。〈凡一章。〉

「凡治曆，以七政經緯度分為本。欲治七政經緯度分， 以恆星度分為本。欲察恆星，得其所居定處，必用測 星之法。」測星之法有三：其一，用太陰。「用太陰者，令太 陰居太陽恆星之間。早測則太陽未出，先測星與太 陰之距度；既出，即測太陰與太陽之距度；晚測則太 陽未入，先測陰陽之距度；既入，即測太陰與星之距 度，各以兩測合推之，得恆星之度分也。其二，用器器 者，水漏、自鳴鐘等一切定時之器，細考恆星遇子午 線時刻，並測其高，又別求太陽所躔本度，因得恆星 經緯之度也。」其三，用太白。用太白者，略同前《太陰》法， 早則先測恆星太白之距，次測太白、太陽之距，晚測 反是，亦各以二距推得恆星度分也。問此三法孰愈？ 曰：「太白為愈。用太陰者，古法也。而未盡善者有三：太 陰之體大，欲測其中點甚難，欲測其邊亦復未易，一 也；本行疾速，先與太陽同測，次與恆星同測，兩測之 間，所過時刻，又自有經行度分，二也；太陰有視差，早 晚間高度愈寡，差度愈多，三也；用器者近世之法，若 人器俱精，多能巧合」，顧其用法繁細，而又多風塵寒 熱之變，亦難保其必合也。若用太白，則近歲之法，較 前二為勝者，其體小，測以窺筩則全見之，行度遲緩， 兩測之間遷變甚少，又視差絕微，通無乖誤之緣也。 《測法》曰：「午後太陽未入，得并見太白時，即測其兩相 距度分。《器用紀限大儀》，一人從通光定耳中窺太白 之體」，一人從通光游耳上取太陽之景次數。儀邊兩 距，即日星之距。又同時用渾儀求其出地平上之兩 高弧及其距赤道之兩緯度。次於日入後，既見恆星， 更依前法求太白與恆星之距度及其兩高弧、兩距 赤緯度。仍併識兩測相距之時刻，推兩測間太白經 行分秒加減之，即得三曜之各定度分，即「得太白左 右太陽與恆星相距之定度分也。」既得此星所躔赤 道經度，又先巳測得距赤緯度，因推得其黃道經緯 度，又用此一星遍測餘星，其經緯度分悉可得矣。西 土士《苐谷》七八年積習此法，度越倫軰，每連日比測， 又早晚並測，必求太陽與太白晚測所居高、所居緯 度，及離地遠近。比次日早測所得，一一符合乃已。何 者？高度同，則視差亦同，以東補西，即不必計視差故也。

《獨測恆星法》第二。〈凡五章。〉

以太白居中左右測恆星太陽之距度，必用兩測，一 求太白距太陽，一求太白距恆星也。然須連日比測， 須早晚並測者，欲以相等之兩視差相補，可不論視 差，此簡法也。今不用比測並測，或早或晚，一測即得， 故名「獨測。」此則必論視差本法也。

求太陽經度

萬曆十年壬午，西二月二十六日申初二刻，《苐谷》用 紀限大儀測太白、太陽之距，得四十六度一十○分 三十○秒。又用渾儀，得太白在赤道北一十五度二 十一分四十○秒。於時太陽在地平上一十五度一 十分，太白高四十八度三十分。〈二測亦用渾儀或象限儀〉因考《太 陽》經度，查本表得娵訾一十七度四十九分四十二 秒，是其實躔。而今求視躔，於法減太陽之東西差二 分一十一秒，為在本宮一十七度四十七分三十一 秒。其《視經》總度，得三百四十八度四十七分三十秒。 〈總度皆從春分起筭〉次查本表，得其緯度分。依法以視差相加， 得視緯偏南四度五十二分一十五秒。更有太白前 見測視緯度及與太陽相離經度，則得所求二總經 度。差如下文：

求太白高下視差

從地半徑所得，「故為高下視差。」

欲推太陽與太白之經度差，必先求太白之東西視 差。然太白之視差有二：一為高下差，一為東西差。又 先從高下差，以得東西差。如左圖：太白居本天為甲， 地心為丙，地面為乙，成甲乙丙三角形。次引長甲乙。

圖

圖

至丁從丙作丁丙垂線成乙丙丁三角形此形有乙丙為地半徑全數丁為直角乙內與乙外兩角等

乙內者丁乙丙角也乙外者甲乙戊角也乙外角為太白高之餘弧角

依三角形法得丙丁線為六六二六二〈全數十萬〉又甲丙

丁三角形內之甲丙線，為太白離地心，其相距以地 半徑為度，得八百一十五，為半徑全數。又先有丁直 角及丙丁線，即推得甲小角二分四十八秒，為太白 之高下視差。

求太白東西視差。〈即《經度視差》。〉

既得「高下差，因，以之求東西差。」〈亦名經度視差〉如左圖，甲為 天頂，亦為地平，辛壬之極，己庚為赤道，其極乙太白 在戊，其高下視差為丙戊弧，即有甲乙戊三角形。其 甲乙為地平，赤道兩極之差，於本地為三十四度○。

圖

圖

五分一十五秒是其北極出地度之餘弧也戊甲為太白出地平高度之餘弧四十一度三十○分乙戊為太白在赤道北緯度之餘弧七十四度三十八分二十○秒以曲線三角形之法因其三邊求其角得本三角形之戊角為九度

四十八分。又於視差丙向丁作垂線，成丙丁戊小三 角形，有丁直角，有戊銳角。又有先所得丙戊視差弧 二分四十八秒。依此用曲線三角形法，得其兩角與 對角之一線，可推其餘邊餘角，得所求丙丁線三十 二秒，為太白之經度視差。

「丙丁線」 ，小圈弧也，與黃道平行。

求太白與太陽經度差

視差既定，次求經度差如左圖甲為赤道極，甲乙甲 戊俱過北極之大圈弧，乙為太陽，丁為太白，乙丁為

圖

圖

兩視處之距弧丙乙丁戊為各距赤道之度即成甲乙丁曲線三角形也今欲求甲角以得赤道之經度差丙戊依前法用三邊求角三邊者甲丁為太白距赤道之餘度甲乙為太陽距赤道之緯度帶一象限乙丁為二測之距度即三

邊具而因以求得甲角，知太白離太陽之赤道經四 十一度五十四分五十八秒，更加入太陽之《視經》總 度。

從春分起算，為三百四十八度四十七分三十○秒。

及太白之《視經重差》。

《重差》者，「一為黃道經差三十二秒，一為赤道差三十○秒。」

則自春分起。數減周，得太白所在，為實，經三十○度四十三分三十○秒。

加減視差訖，乃得《實經》。

求畢宿大星赤道經緯度。

本日戌初初刻，測畢宿大星，其西距太白三十○度 五十九分，其赤道緯一十五度三十六分，太白高二 十七度三十○分，在赤道北一十五度二十五分一 十○秒。今求兩距之赤道經度，差如左圖：丁戊為赤 道，甲為赤道極，乙為太白，丙為畢大星，甲乙為太白 緯度之餘弧，甲丙為畢大星緯度之餘弧，乙丙其兩。

圖

圖

測之距弧依上法得甲角三十二度一十一分○六秒兩星之經度差也又依此時刻定太白之本行為是日合行五十七分先後兩測間得八分一十八秒以加太白之實經度又以後測之高下視差再用前高下差圖求得三分四十

五秒以求東西視差，亦再用前《東西差圖》求得二分 ○七秒，以減太白之實經度，共得春分至太白之視 經三十○度四十九分四十一秒。以加太白距畢大 星之視經三十二度一十一分○六秒，得此星離春 分六十三度○○四十七秒。

《重測恆星法》第三。〈凡四章。〉

前法因視差之煩，恐有誤，不如早晚左右測之，兩得 數，相除相補，簡而易就，所謂「重測」也。

求《婁宿北星赤道經緯度》。

萬曆十四年丙戌，西十二月二十六日申初二刻，苐 谷測得太白距太陽四十六度三十○分。太白在赤 道南一十一度一十五分三十○秒，高二十三度，正 太陽高三度。其距赤道，查本表得在南二十二度四 十一分三十○秒，躔星紀一十四度五十一分五十 三秒，《總經》得二百八十六度○八分四十二秒。〈春分起筭〉 如左圖，甲為赤道南極，乙為太白，丙為太陽，甲乙為 太白距南之餘弧七十八度四十四分三十○秒，甲 丙為太陽距南之餘弧六十七度一十八分三十○。

圖

圖

秒乙丙為兩測之度差依三角形法推得甲角四十七度二十一分○五秒為太白距太陽之經度差其總經為三百三十三度二十九分四十七秒再於本日申正三刻求婁宿北星距太白經度差得五十二度二十一分太白高二十

○度三十○分。《兩測間》，太白之本行四分五十四秒。 以加經度差，總得太白經度三百三十三度三十四 分四十一秒。以加二星經度差，減周，約存婁宿北星 赤道視經二十五度五十五分四十一秒。

求角宿距星赤道經緯度。

又戊子年西十二月十五日巳初初刻，測得太白距 太陽四十六度三十六分，出地平高二十度，居赤道 之南十四度○四分，太陽高三度，躔星紀三度五十 三分四十一秒，在赤道南二十三度二十八分○二。

圖

圖

秒其總經二百七十四度一十四分四十九秒如圖甲為南極乙為太白丙為太陽丙甲為太陽緯度之餘六十六度三十二分乙甲為太白緯度之餘七十五度五十六分乙丙為兩測之距四十六度三十六分依法推得乙丙距之經

度差為丁戊，四十八度二十六分一十八秒，以減太 陽經度，餘二百二十五度四十八分三十一秒，為太 白之總經度。

本日辰初三刻，先測太白距角宿距星二十九度三 十三分三十○秒，居赤道南一十四度○二分，出地 平上一十九度。今依前圖，乙為角距星，丙為太白，餘 同上。乙甲為角距星緯度之餘，弧八十一度○二分 四十五秒；丙甲為太白緯度之餘，弧七十五度五十 八分；乙丙為兩星相距二十九度三十三分三十○。

圖

圖

秒依法推得甲角二十九度四十四分二十一秒為兩星之經度差又兩測間太白赤道度三分四十七秒以減前太白之總經度得二百二十五度四十四分四十四秒再減角距星與太白經度之差得總經一百九十六度○分二十

三、秒

再求角宿距星赤道經緯度。

前借西土所測三星之度，仍用三角形証之，百簡其 二三，以明法之密合。其法再取角距星以較兩年所 測，而定其準數。如前。丙戌年測婁北星，得二十五，經 度五十五分四十一秒。若加婁角二星元經度之差， 一百六十九度五十一分五十一秒，即丙戌年角距 星之經度，共得一百九十五度四十七分三十二秒。 「此比戊子年所得之一百九十六度○分二十三秒， 差一十一分一十一秒。」論《赤道經度》之星差，兩年間 不得有此。所以然者，因當日所測之星及太陽，皆居 赤道南，與地平相近，其視差為多。繇有清蒙之差，地 半徑之差，其視差愈多故也。雖然，其東西兩測之高 度既同，距度又同，若以前差分秒平分之減多益少， 即得平矣。故於戊子年減恆星差五十秒，以進一周， 丙戌年反加之，以退一周，折中為丁亥年冬至之後， 角距星之經度，有一百九十五度五十三分五十八 秒，與前獨測畢大星之經度正相合。何者？彼所得六 十三度○分五十三秒，而本星距角距之元經，為一 百三十二度四十八分一十○秒。兩測之相距，六年， 更加經五分。

恆星東行，每年五十一秒，六年得五分○六秒。《赤經》略同。

并之，得角宿距星，丙戌年。兩測為俱在同度同分，僅 隔五秒矣。

證獨測不如重測之便

測恆星之經度。向所云「獨測為本法，重測為簡法」，其 大端矣。重測之為簡法者，獨測之求視差甚難，重測 則不論視差也。所以不論視差者，先於西邊測太陽 之高度，後於東邊測太陽之高度。兩高度既同，即其 距赤道兩率不甚相遠，而太白之兩高度與其兩距 度亦然。即有偏斜、微細難推，可勿論也。此兩測所得 數，若有贏縮，則兩視差所為矣。而兩測之高同、緯同， 則視差必同。若依本法推論，視差所得數，於兩測一 宜減，一宜加。今以贏縮之總率平分之，加一於此，減 一於彼，損有餘，補不足，適得其平，與兩推視差何異 焉？故曰「重測則不論視差。」《苐谷》之新法，甚為簡捷者 也。

「以赤道之周度察恆星之經度」第四。〈凡二章。〉

近黃赤兩道有大星任定若干為距星。用前測法，或 自西而東，或自東而西，求其兩測之距度及其距赤 道之緯度，即用三角形法，推得其經度差。如是相連 綴求之，以迄一周，所得各赤道經度。總之，合於赤道 周。即如所測各距星之經度，俱為密合。用此距星為 眾星之界，測量推算，鮮不合也。

先左旋求四大距星之經度。

今借用萬曆十三年乙酉《苐谷》所測之星以為法，如 左圖：甲乙丙為極分交圈，乙丙為赤道，甲為赤道極， 庚為角宿距星，距河鼓中星，巳，九十七度五十○分， 在赤道南八度五十六分二十○秒。河鼓已距婁宿 北星，丁九十○度一十五分，在赤道北七度五十一 分三十○秒。婁北丁距北河東星，戊七十四度四十 五分三十○秒。在赤道北二十一度二十八分三十 ○秒。北河東戊又距角距星九十○度四十六分二

圖

圖

十○秒距赤道二十八度五十七分左旋一周連綴測得各星經度總之合於赤道周即各測俱不謬而可用為距星以測眾星矣依前法先推甲己庚三角形其第一邊甲己為河鼓中星緯度之餘八十二度○八分三十○秒第二邊

甲庚為北極至赤道南之角大星，共九十八度五十 六分二十○秒。第三邊庚己為兩星之距度，依上測 為九十七度五十○分，用三角形法，推得九十六度 四十五分○九秒，為甲角之弧，即兩星相距之赤道 經度也。次推甲己丁三角形。有第一甲己，邊有第二 甲丁，為北極至婁北，得六十八度三十一分三十○ 秒。第三己丁河鼓中婁北之距，依上測為九十○度 一十五分。依法推得甲角之赤道弧九十三度二十 二分五十八秒。又轉推甲丁戊在左，甲戊庚在右，兩 三角形，其甲戊六十一度○三分為同用邊，餘邊皆 見上文。依法推甲角左對弧八十三度五十七分三 十三秒，右對弧八十五度五十四分一十八秒。此四 星相距之各經度差，并之，得三百五十九度五十九 分五十八秒，以較赤道全周，止差二秒。若以秋分為 界，則於半周減一十五度五十二分一十八秒，為秋 分與角大星之距度。次加各星之經度差，以合於全 周。

《後右旋》求六大距星之經度。

上文「隨恆星之本行，自西而東，測得其經度。此自東

還西反測之，以證其密合。」亦用角宿距星為首，依萬 曆乙酉所測赤道，與前解不異。所得諸星距度及赤 道經緯度，若數一二，於眉睫之下也。

六大星　　　距赤道度　　　分　　　　秒， 乙角宿距星　南　　八、　　　五十六、　　二十； 丙軒轅大星　北　　十三、　　五十八　　○； 丁井宿距星　北　　二十二、　三十八、　　三十， 戊婁宿大星　北　　二十一、　二十八、　　三十， 己室宿大星　北　　十三　　○、　　　　四十， 庚河鼓中星　北　　七、　　　五十一、　　二十 六大星　　　相距　度　　　分　　　　秒， 乙角宿距星　南　　五十四、　二　　　　○， 丙軒轅大星　北　　五十四、　三十三、　　四十五； 丁井宿距星　北　　五十八、　二十二　　○ 戊婁宿大星　北　　三十四、　三十七　　十五。 己室宿大星　北　　四十七、　四十九、　　二十。 庚河鼓中星　北　　九十七、　五十　　　○

圖

圖

六距星用大三角形輳甲者六角

第一乙甲丙形從甲過赤道至乙共九十八度五十六分二十○秒甲丙為軒轅大星距赤道之餘七十六度○二分乙丙為二星之距五十四度○二分推得甲角對二星之經度差

四十九度，一十九分二十○秒。

第二丙甲丁形，先有甲丙，其甲丁為井宿距星距赤 道之餘，六十七度二十一分三十○秒；丙丁為二星 之距，五十四度三十三分四十五秒，推得甲角弧五 十七度○四分一十○秒。

第三丁甲戊形，先有甲丁，其甲戊為婁宿北星距赤 道之餘，六十八度三十一分三十○秒，丁戊為二星 之距，五十八度二十二分，推得甲角弧六十三度二 十八分三十○秒。

圖

圖

第四戊甲己形先有甲戊其甲己為室宿距星距赤道之餘七十六度五十九分二十○秒戊己為二星之距三十四度三十七分一十五秒推得甲角弧四十四度五十八分

第五己甲庚形先有甲己其甲庚為河鼓中星緯度

之餘，八十二度○八分四十○秒。其己庚為二星之 距，四十七度四十九分，得甲角弧四十八度二十五 分。

第六庚甲乙形，先有兩腰，其庚乙為二星之距，九十 七度五十○分，得甲角弧九十六度四十五分一十 ○秒。巳上所得六經度差。并之，得三百六十度，即赤 道周。若從二分起算，則先定近分第一星近分之度， 以加減前測，所得不異。今依上述萬曆乙酉所測春 分以後總經度如左：

星名　：《赤道經度　　》分　　　秒。

婁宿大星　二十六　　　○、　　　三十

畢宿大星　六十三、　　　三　　　四十五 井宿距星　八十九，　　　二十九，　一十

北河東星，　一百九、　　　五十八　○。

軒轅大星　一百四十六、　三十二，　四十五 角宿距星　一百九十五，　五十二，　一十八 河鼓中星　二百九十二、　三十七、　二十。

室宿距星　三百四十一、　二　　　三十

星名　：赤道緯度　　分　　　秒：

婁宿大星：　二十一、　　　二十八、　三十

畢宿大星，　十五、　　　　三十六，　十五

井宿距星　二十二、　　　三十八、　三十

北河東星：　二十八，　　　五十七，　四十五 軒轅大星　一十三，　　　五十七，　四十五 角宿距星：　八，　　　　　五十六，　二十

河鼓中星：　七　　　　　五十一　二十。

室宿距星　一十三　　　○、　　　二十

以恆星赤道經緯度求其《黃道經緯度，第五》。〈凡五章。〉

「前定赤道上之恆星經緯度」，可用以推考七政矣。欲 求備法，須更求黃道上經緯度也。蓋黃道上恆星之 緯度終古不易，其經度雖隨時變易，而每星相距之 經度差亦終古如一，無相離、無相就也。所以然者，恆 星本行之極，即是黃道之極。故用赤道者，為其與天 元密合；用黃道者，為其與本行密合。二道、二極、兩經 「兩緯，兼而用之，七政遠近，灼然不爽矣。」欲推其理，非

圖

圖

三角形無繇得之今更依前所測諸星申明此法如左

星居兩道之北

如圖外周為極至交圈丁己為赤道戊庚為黃道乙為赤道極丙為黃道極甲為婁宿北星之本位今設赤道距度甲丁經度辛丁

圖

圖

以求黃道經度辛戊緯度甲戊其法用甲乙丙三角形有乙丙邊〈兩極相距〉有甲乙。〈赤道緯度之餘〉有乙角。

對邊丁辛己丁辛為赤道經度辛為春分辛己為象限

依三角形法先求得甲丙八十度○三分為黃道緯

度之餘次，求得丙角。其弧戊壬得五十八度○六分 五十○秒，為黃道經度之餘。壬，夏至也；辛，春分也。以 戊壬減壬辛象限，得戊辛三十一度五十三分一十 ○秒，為黃道經度。又以甲丙減丙戊象限，得甲戊九 度五十七分，為黃道緯度。求餘星倣此。其居黃赤道 南北左右位置不同，別用三角形求之。今略舉如左：

星居兩道之中

如甲為畢宿大星，有赤道緯度，甲丁依前用甲乙丙 三角形之法，求得丙極出弧過黃道，自戊至甲共九。

圖

圖

十五度三十○分五十一秒即象限外五度三十○分五十一秒為黃道之南距緯度而丙角之弧戊壬二十六度○二分以減象限得戊辛六十三度五十八分為畢大星之黃道經度

又如甲點為井宿距星其

甲乙丙三角形求甲丙法，以乙丙、乙甲兩邊及乙角， 推得甲丙九十度五十二分五十七秒，為南距緯度。 其在黃道南者止五十二分五十七秒，其丙角亦止 二十八分四十○秒，其餘辛甲即本星之黃道經度 也。

星居兩道之南

如角宿距星，居黃赤二道之南，圖中甲乙丙三角形， 與上相似，即推法亦同，但乙丙則南極耳。形之甲丙 弧八十八度○一分，即甲星在黃道南一度五十九。

圖

圖

分是其緯度而丙角之對弧庚戊七十一度五十六分五十○秒即黃道經度自戊至秋分辛得一十八度○三分一十○秒

星居兩道相交之左

左圖則辛為春分辛己為黃道辛庚為赤道冬至移左夏至移右而經度亦從

圖

圖

左起算故甲乙丙三角形與上第一圖正相反上求甲丙此則甲乙上求丙角此乙角也如甲為河鼓中星依法求得乙極至甲六十○度三十八分三十秒即甲丁二十九度二十一分三十秒為黃道緯度而乙角之弧丁己一百五十

圖

圖

五十四度○四分減象限己辛得辛丁六十四度○四分為距春分之黃道經度若甲為室宿距星依法求得乙極至甲七十○度三十四分即甲丁一十九度二十六分為黃道緯度而乙角丁己一百○七度有奇可推距春分之經度

圖

圖

星居兩道相交之右

此圖則辛又為秋分餘皆如前一二圖而甲星在秋分辛夏至癸之間即其經度必過一象限如甲為北河東星依法求得甲丙八十三度○二分○八秒即緯度在黃道北六度五十七分五十二秒而丙角於

圖

圖

一象限外加一十七度三十○分二十六秒為其黃道經度若甲為轅軒大星即甲丙之餘甲戊在黃道北止二十六分三十○秒為其緯度而丙角之弧於夏至癸一象限外加五十四度○四分四十○秒為其黃道經度

星名　：《黃道經度　　　　分　　　秒》。

婁宿北星：　北　三十一，　　　五十三　○， 畢宿大星　南　六十四　　　○　　　○， 井宿距星　南　八十九，　　　三十一，　二十， 北河東星　南　一百七，　　　三十，　　三十， 軒轅大星　北　一百四十四，　四　　　四十， 角宿距星：　南　一百九十八，　三　　　○， 河鼓中星　北　二百九十五，　五十六　○， 室宿距星　北　三百四十七，　四十四　○。

星名　：《黃道緯度　　　　分　　　秒》：

婁宿北星：　北　九　　　　　五十七　○， 畢宿大星：　南　五　　　　　三十一　○， 井宿距星：　南　○　　　　　五十三　○， 北河東星：　南　六　　　　　五十八　○， 軒轅大星：　北　○　　　　　二十六，　三十， 角宿距星：　南　一　　　　　五十九　○， 河鼓中星：　北　二十九，　　　二十一，　三十， 室宿距星：　北　一十九，　　　二十九　○

《以恆星測恆星》第六。〈凡二章。〉

前以「太白求恆星，簡知太陽所在」，因是推定各星度 數，其理著明矣。今既得恆星為界，即不必以太陽與 距星比測，直以星相比，可得其實躔度數也。

測近赤道之恆星

凡恆星近赤道四十度以下，藉儀器測之，聊可省功， 太遠即不可。蓋渾儀中圈，正合天元赤道，乃至地平、 過極等圈，皆切對其所當度分。所以近赤道諸星，不 論在何方向，即可指本星之赤道經度差及其距度 也。但須用二星左右同見，先得其遠近度差，依法求 得第三星之真經度。

《真經度者》，從降婁起算至本星。

「若彼此分秒相符，即為密合。若有微差，則平分其較， 以多益寡。」假如測井宿南第二星，得赤道北緯一十 六度四十○分，左有軒轅大星，其北緯一十三度五 十七分四十五秒，相距五十一度一十一分，即所求 經度差為五十三度○八分三十○秒。此應減於先 得之軒轅經度，而存九十三度二十四分一十五秒， 為是井二星之經度也。〈春分起筭〉右有畢宿大星，其北緯 一十五度三十六分一十五秒，相距二十九度○九 分，即所求經度差三十○度二十一分一十五秒，應 加於畢宿大星之本經度，乃得井二星之經九十三 度二十五分也。兩測相比，則右方所得數，較餘四十 五秒減半，以益左，得九十三度二十四分三十六秒， 為井二星赤道上真經度矣。

今更求黃道經緯度，即以所得赤道經緯度，依前第 五題法，即得。井二星甲之經度，在鶉首三度一十八。

圖

圖

分五十○秒其南緯六度四十八分三十○秒居黃赤二道之間其餘星各依本方本向或南或北各依三角形法推算俱倣此

測近兩極之恆星

隆慶六年壬申有客星甚大在策星東北甚近苐谷詳究其經緯度先測定四周諸星然後與本星兩兩相比即得其實所今先用所測王良西星以明其法按王良西星距婁北星四十一度二十○分四十五秒距北河南星七十七度二十五分如上圖甲為婁北星乙為北河丙為王良西星從黃道極丁出弧過各星至戊至己至庚成甲乙丁甲乙丙乙丙丁三三角形今所求者為王良西星距黃道之餘弧丁丙及丁角以得黃道上之戊庚弧定其經度也

先論甲乙丁三角形其兩腰弧為二星距極之弧即其距黃道之餘弧也一為

「八十○度○三分一，為八十三度二十二分。其乙丁

甲角之弧，戊己則二星之黃道經度，差為七十五度 三十七分。」如前法得甲乙底七十四度四十五分○ 八秒，又得乙角八十一度二十七分一十五秒。 次論甲乙丙三角形，其腰線即王良西星與二星之 距，而底線即上甲乙。因推甲乙丙角四十二度三十 四分一十八秒，而存丙乙丁外角三十八度五十二 分五十七秒。〈下文用此〉

永論乙丙丁三角，形前已得乙丙，乙丁丙弧及乙角，

圖

圖

因推得丙丁弧三十八度四十五分二十二秒其餘弧丙庚為王良西星距黃道之緯度又推得丁角七十八度○八分三十○秒是王良西星與北河南星之黃道經度差真經度所出也若更求其赤道經緯度即因所得度分如上圖

之甲丙線及丙角，依前第五題法，即得本星之赤道， 經三百五十六度四十三分二十○秒。其北緯五十 六度四十八分三十○秒，餘星皆依此法。

《測恆星之資》第七。〈凡一章。〉

測恆星，測七政，躔度，公理也，而有四資：一曰測器，二 曰子午線，三曰北極出地度分，四曰視差。四資既具， 非其時又不可測焉。測器者何也？凡測星有三求：一 求其出地平上度分，二求其互相距度分，三求其距 黃赤二道之何方、何度分。所用器亦有三：一為過天 頂之圈，如象限儀、立運儀等，此為測地平高度之器； 「一為紀限儀」，此為測兩距度之器，一為渾天儀，南北 觀象臺所有即是，是為兼測二道經緯之器。今所用 測星者，則紀限、渾天二儀，而非大不得準，非堅固不 得準，非界畫均平，安置停穩，垂線與窺筩景尺，一一 如法，亦不得準也。子午線者，七政行度，升之極而降 之始也。北極出地者，凡用儀，必以儀之極與本地之 高極。〈高極者出地上之極也〉「相當，而後各經緯皆相當，乃始展 轉測候焉。若無子午以正東西升降，無高極以正南 北高下，即一切綴算之法無從得用。」故二者測天之 本也。視差者何也？凡七政之視差有二：一為地半徑 差，一為清蒙氣差。地半徑差月最大，日、金水次之，火、 木、土則漸遠漸消。恆星天最遠，地居其中，止於一點， 故絕無地半徑差，而獨有清蒙之差。清蒙地氣，去人 甚近，故不論天體近遠，但以高卑為限。星去地平未 遠，人目望之，星為此氣所蒙，不能直射人目，必成折 照，乃能見之。一經轉折，人之見星，必不在其實所，即 星體在地平之下，人所目見，乃在其上也。〈說見日躔曆指〉迨 升度既高，蒙氣已絕，則直射人目，是為正照，雖星月 之間，微有濕氣，不能為差也。試用一星於地平近處， 測其去北極之度，迨至子午圈上又測之，即兩測必 不合。或用兩星於地平近處，測其距度，迨至子午圈 上又測之，即兩測亦必不合。此其證也。此氣晴明時 有之，人目所不見，而能曲折相照，升卑為高，故名「清 蒙。」若雲霧等濁蒙，直是難測，不論視差矣。苐谷累年 測候，妙悟此理，剏立差分，恒星視差比日躔視差更 弱，止近地平二十度以下，乃能覺之。表如下方 恒星高度　○，　一、　二、　三、　四、　五、　六、　七、　八、　九、　十　十、一、　十二、　十三、　十四、　十五、　十六、　十七、　十八、　十九、　二十， 恒星分　三十、　二、十一、　十五、　十二、　十一、　十　九、　八、　六、　六、　五、　五、　四　四　三　三　二　二　一　一　○　○， 視差秒　○　三十，　三十，　三十　○　○　○　十五　四五　○，　三十　○，　三十　○　三十　○　三十　○，　十五　三十。 作此表者，其本方極出地之度，與此方不等。且視差 亦隨天氣各有多寡厚薄，但數既密微，測得其時，則 此表可共用之。所謂「時」者，如雲霞霧霿無論已，即使 晴明時日，而二十度以下蒙氣，乃所必有。若所測兩 星「俱在二十度以上，即可不論視差。若一在二十度 上，與《蒙氣》相絕，一在二十度下，居蒙氣之中，則近地 平之星，必升卑為高，而成視差，兩星之經度非真率 矣。至若日躔元枵，於時為立春，於候為東風解凍，濕 氣尤盛。此際測星，其視差必多於他時，更宜消息加 減之也。」此四資者，為測星所須，舉其大略。若全理全 用，具載《本論》。

《測恆星之器》第八。〈凡二章。〉

《測量全義》之末篇，論諸測器略備矣。此所系獨測候 恆星二器者，因上文每言測法，必先明器理，然後能 通其言意也。

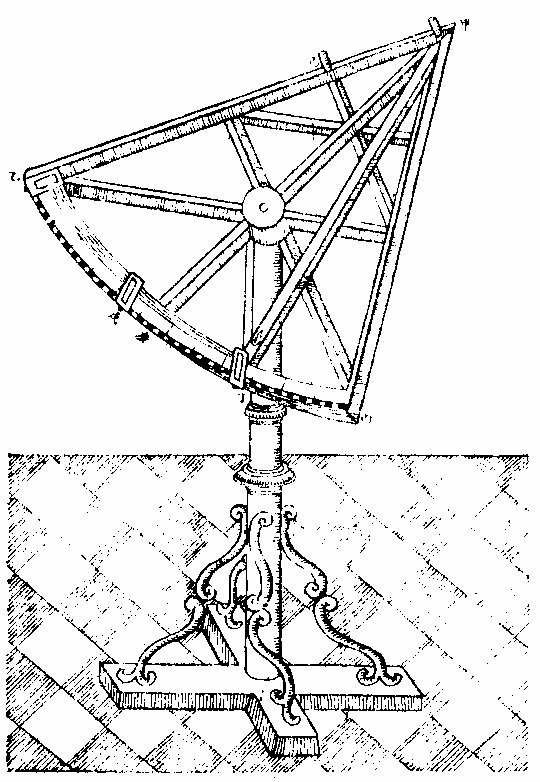
測恒星相距之器

測恆星相距之器圖說

如前圖。甲乙丙為全圈六分之一，名「紀限儀」者，曆家 以六十為紀法，以別於四分一之象限也。甲為全圈 之心，乙丙為紀限之弧，分六十度，度分六，分十二或 三十，任儀大小作之，儀愈大分愈細，即愈善耳。甲丁 尺為度尺，樹圓表於甲以為尺樞，其末丁游移弧上 以定度分切度分之處，剡其半為中線，以直當甲心 之一點。丁上立一通光耳，耳上於中線兩旁各作一 罅，各與中線平行，兩罅之間，與甲表之徑等，是耳隨 尺游移，故名「通光游耳。」又於乙上立一耳，常定不移， 是名「通光定耳。」又別作一耳，用則加之，否則去之，是 名「通光設耳。」三耳之用不同，其制一也。又於己上立 一小表，弧之上，去乙二十度為戊，去乙丙各三十度 為庚，己戊線與甲庚平行，使從戊闚己，從庚闚甲，其 度分等。而通光設耳之本所則戊也。全器以架承之， 或為圓球架，或為三樞架，令上下左右偏正無所不 可，以便展轉測諸曜之距度分。《測法》：先定所測之二 星，順其正斜之勢，以儀面承之，以搘杖支之。次令一 人從《定耳》之一罅窺甲表同方之一邊，令目與表與 第一星相參直。又一人從游耳窺第二星亦如之。次 視兩耳下兩中線之間弧上距度分，即兩星之距度 分也。若兩距度分絕少，難容兩人並測，即加設《耳》於 戊，以戊己當乙甲，向己表窺第一星，而丁甲度尺對 第二星，如前從庚右數之，即所測之距度，因戊己與 庚甲「為平行線」故也。凡測日與月，月與星，星與日，皆 倣此。但日光照耀，表景多虛淡不明。宜用展縮木筩 一具，加度尺之上，以束光聚影，則灼然易見矣。

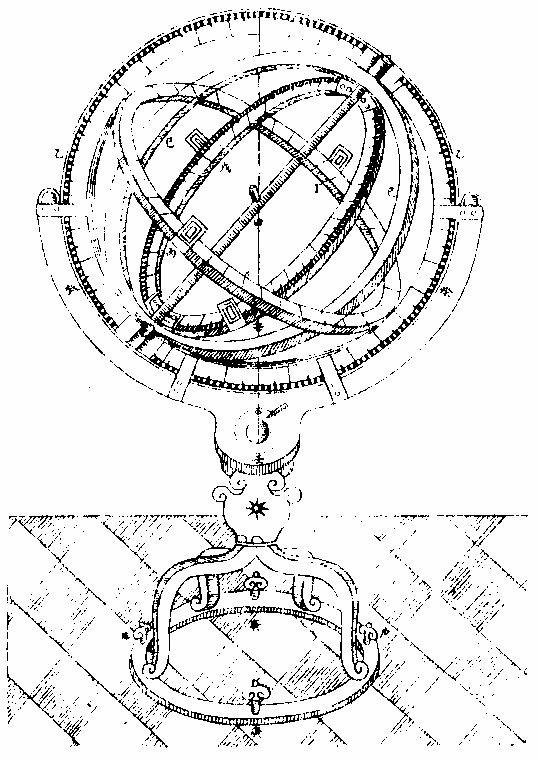
測恒星赤道經緯度之器

測恆星赤道經緯度之器圖說：

「如前圖。乙為子午圈，周分三百六十度，游移架上，以 就本方北極出地之高，平分其周而設之軸，平分其 軸而設之表，當天頂而設之垂線，下置垂權，至於壬 而止，以取平也。架之下設螺轉之槷四以為足，展轉 視垂權而高下之」，以取平也。軸之兩端入於乙圈之 鑿，欲其利轉也，其交於己圈也。己圈之交於丙丁圈 也，持之欲其固也。丙丁圈者，赤道也，平分兩極，而居 於己圈之中界，故又名中圈也。己與丙丁兩圈為一 體，旋轉相從，而兩圈之內，又設為戊辛之圈。戊辛與 外圈同軸，自為旋運，不交於外圈。而丙丁戊辛兩圈 之上，各設兩游耳。游耳者，可離可合，百游無定之通 光耳也。兩圈之各兩面，皆平分為三「百六十，以定度 分。」其測星也，用赤道圈求經度法，以兩通光耳一定 焉，一游焉，一人從定耳窺軸心之甲表，與第一星參 直，一人移游耳展轉遷就，窺甲表與第二星參直。兩 耳間之度分，即兩星之真經度差也。用戊辛圈求緯 度，亦以《通光耳》遷就焉。若測向北緯度，即設耳於赤 道南；測向南緯度，即設耳於赤道北，皆準諸軸心之 甲表，令目與表與所測星參直乃止。次簡《游耳》下本 圈之度分，在赤道圈或南或北凡若干，即本星之距 赤道南北度分。〈按以上原本作曆指卷一誤當為原本曆指卷二恆星之一